Самая большая сумма – Самая большая банкнота в мире по номиналу и покупательной способности

Содержание

Системы наименования чисел — Википедия

В европейской традиции исторически сложились два варианта построения системы наименования чисел.

Термин «миллион» итальянского происхождения и встречается уже в первой печатной арифметике (анонимной), вышедшей в итальянском городе Тревизо в 1478 году, и ещё ранее в нематематической книге путешественника Марко Поло (умер в 1324 году), а в форме «миллио» — уже в рукописи 1250 года.

В рукописи французского математика XV века Никола Шюке впервые появляются термины «биллион» — 10¹², «триллион» — 10¹⁸ и дальнейшие; в печатном руководстве биллион в значении 10¹² появляется в 1602 году.

В XVII веке во Франции начали употреблять короткую шкалу: «биллион» — 10⁹, «триллион» — 10¹² и т. д.

Слово «миллиард», имевшее вначале значение 10¹², получило значение 10⁹ (тысячи миллионов) в «Арифметике» Траншана (1558) и употреблялось во Франции в XIX веке наравне со словом «биллион». В Германии это слово вошло в употребление лишь после получения от Франции 5 миллиардов контрибуции после франко-прусской войны 1871 года.

Для чтения многозначных чисел анонимная рукопись 1200 года впервые рекомендует разбить цифры на группы по 3 или отмечать группы точками вверху или дугами; это же затем рекомендует Леонардо Пизанский (1228). К этой системе приходят и последующие авторы.

Использование систем наименования чисел в мире:

короткая шкала длинная шкала

обе шкалы другие системы

В России первоначально была введена система наименования чисел с длинной шкалой, и, по-видимому, в печатном виде впервые в 1703 году в «Арифметике» Л. Ф. Магницкого. Однако в конце XVIII века, в царствование императора Павла I, вслед за Францией произошёл переход на короткую шкалу. Так, в опубликованном в 1798 году переводе части первой — «Арифметика» — «Курса математики» Этьенна Безу введена система наименования чисел с короткой шкалой, при том, что ещё в опубликованной в 1791 году книге «Арифметика или числовник» Н. Г. Курганова (1725 или 1726—1796) используется длинная шкала.

В 1948 году IX Генеральная конференция по мерам и весам приняла предложение Международного комитета мер и весов, рекомендующего для европейских стран применение длинной шкалы. Франция вернулась к системе с длинной шкалой, а в России продолжалось использование системы с короткой шкалой, которая была заимствована во Франции ранее. Однако, использование длинной шкалы предусматривается рекомендацией Совета экономической взаимопомощи PC 2625—70 «Основные математические обозначения»

[1], где приводятся основные математические обозначения, употребляемые в нормативно-технической документации, научной и технической литературе и в школьных учебниках. Последнее позволяет утверждать, что официально во всех странах, образовавшихся после распада СССР, с 1948 года действует именно длинная система наименований чисел, хотя фактически продолжает применяться короткая система.

В случае короткой шкалы все названия больших чисел строятся так: в начале идёт латинское числительное^[2], обозначающее степень тысячи, а в конце к нему добавляется суффикс «-иллион». Исключение составляет название «миллион», которое образовано от латинского числительного mille «тысяча» при помощи увеличительного суффикса «-он» -one). Так получаются числа — миллион, биллион^[3], триллион, квадриллион, квинтиллион, секстиллион и т. д. Система наименования чисел с короткой шкалой используется в России^{[источник не указан 25 дней]}, Белоруссии, Украине, США, Канаде, Великобритании, Ирландии, Австралии, Бразилии, Болгарии, Греции, Румынии и Турции. Количество нулей в числе, записанном по этой системе, определяется по формуле 3·

x+3 (где x — латинское числительное).

Названия чисел в этой системе строятся так: к латинскому числительному^[2], обозначающему степень миллиона, добавляют суффикс «-он», название следующего числа (в 1000 раз большего) образуется из того же самого латинского числительного, но с суффиксом «-ард». То есть после триллиона в этой системе идёт триллиард, а только затем квадриллион, за которым следует квадриллиард и т. д. Количество нулей в числе, записанном по этой системе и оканчивающегося суффиксом «-иллион», определяется по формуле 6·x (где

x — латинское числительное) и по формуле 6·x+3 для чисел, оканчивающихся на «-иллиард».

В настоящее время применяется в большинстве франкоязычных, скандинавских, испаноязычных^[4] и португалоязычных стран, кроме Бразилии.

Таблица от значения к названию[править | править код]

Порядок	Значение	число нулей	Короткая шкала		Длинная шкала		СИ
Порядок	Значение	число нулей	Название	Логика построения	Название	Логика построения	СИ
0	10⁰	0	один	1000^{1 + (-1)}	один	1 000 000⁰
1	10³	3	тысяча	1000^{1 + 0}	тысяча	1 000 000^0,5	кило-
2	10⁶	6	миллион	1000^{1 + 1}	миллион	1 000 000^1,0	мега-
3	10⁹	9	биллион (миллиард)^[3]	1000^{1 + 2}	миллиард (тысяча миллионов)	1 000 000^1,5	гига-
4	10¹²	12	триллион	1000^{1 + 3}	биллион	1 000 000^2,0	тера-
5	10¹⁵	15	квадриллион	1000^{1 + 4}	биллиард (тысяча биллионов)	1 000 000^2,5	пета-
6	10¹⁸	18	квинтиллион	1000^{1 + 5}	триллион	1 000 000^3,0	экса-
7	10²¹	21	секстиллион	1000^{1 + 6}	триллиард (тысяча триллионов)	1 000 000^3,5	зетта-
8	10²⁴	24	септиллион	1000^{1 + 7}	квадриллион	1 000 000^4,0	иотта-
9	10²⁷	27	октиллион	1000^{1 + 8}	квадриллиард (тысяча квадриллионов)	1 000 000^4,5
10	10³⁰	30	нониллион	1000^{1 + 9}	квинтиллион	1 000 000^5,0
11	10³³	33	дециллион	1000^{1 + 10}	квинтиллиард (тысяча квинтиллионов)	1 000 000^5,5
12	10³⁶	36	ундециллион	1000^{1 + 11}	секстиллион	1 000 000^6,0
13	10³⁹	39	дуодециллион	1000^{1 + 12}	секстиллиард (тысяча секстиллионов)	1 000 000^6,5
14	10⁴²	42	тредециллион	1000^{1 + 13}	септиллион	1 000 000^7,0
15	10⁴⁵	45	кваттуордециллион	1000^{1 + 14}	септиллиард (тысяча септиллионов)	1 000 000^7,5
16	10⁴⁸	48	квиндециллион	1000^{1 + 15}	октиллион	1 000 000^8,0
17	10⁵¹	51	сексдециллион	1000^{1 + 16}	октиллиард (тысяча октиллионов)	1 000 000^8,5
18	10⁵⁴	54	септендециллион	1000^{1 + 17}	нониллион	1 000 000^9,0
19	10⁵⁷	57	октодециллион	1000^{1 + 18}	нониллиард (тысяча нониллионов)	1 000 000^9,5
20	10⁶⁰	60	новемдециллион	1000^{1 + 19}	дециллион	1 000 000^10,0
21	10⁶³	63	вигинтиллион	1000^{1 + 20}	дециллиард (тысяча дециллионов)	1 000 000^10,5
22	10⁶⁶	66	унвигинтиллион	1000^{1 + 21}
23	10⁶⁹	69	дуовигинтиллион	1000^{1 + 22}
24	10⁷²	72	тревигинтиллион	1000^{1 + 23}
25	10⁷⁵	75	кваттуорвигинтиллион	1000^{1 + 24}
26	10⁷⁸	78	квинвигинтиллион	1000^{1 + 25}
27	10⁸¹	81	сексвигинтиллион	1000^{1 + 26}
28	10⁸⁴	84	септенвигинтиллион	1000^{1 + 27}
29	10⁸⁷	87	октовигинтиллион	1000^{1 + 28}
30	10⁹⁰	90	новемвигинтиллион	1000^{1 + 29}
31	10⁹³	93	тригинтиллион	1000^{1 + 30}
32	10⁹⁶	96	унтригинтиллион	1000^{1 + 31}
33	10⁹⁹	99	дуотригинтиллион	1000^{1 + 32}
34	10¹⁰²	102	третригинтиллион	1000^{1 + 33}
35	10¹⁰⁵	105	кваттуортригинтиллион	1000^{1 + 34}
36	10¹⁰⁸	108	квинтригинтиллион	1000^{1 + 35}
37	10¹¹¹	111	секстригинтиллион	1000^{1 + 36}
38	10¹¹⁴	114	септентригинтиллион	1000^{1 + 37}
39	10¹¹⁷	117	октотригинтиллион	1000¹⁺³⁸

Таблица от названия к значению[править | править код]

Виленкин Н. Я. От нуля до декаллиона // Квант, 1989, № 3. С. 20.
Депман И. Я. История арифметики // 2-е изд., испр. М.: Просвещение, 1965. 416 с.
Мендаль З. О названиях и начертании больших чисел. // Техника молодежи 1938 г., № 1, стр. 58.
Перельман Я. И. Занимательная арифметика // 1926 год. Ленинград, «Время», 192 c.
Киселев А. П. Систематический курс арифметики // 1912 год.
Безу Э. Курс математики. Арифметика // М., 1806. 191 с. 2-е изд.
Курганов Н. Г. Арифметика или числовник. Часть 1 // СПб., 1791
Магницкий Л. Ф. Арифметика // 1703 год
Керн С. A Zillion Troubles
Козловский С. Самое большое число в мире

Самое большое число в мире

“Я вижу скопления смутных чисел, которые скрывается там, в темноте, за небольшим пятном света, которое дает свеча разума. Они шепчутся друг с другом; сговариваясь кто знает о чем. Возможно, они нас не очень любят за захват их меньших братишек нашими умами. Или, возможно, они просто ведут однозначный числовой образ жизни, там, за пределами нашего понимания’’.
Дуглас Рэй

Продолжаем нашу рубрику САМОГО САМОГО. Сегодня у нас числа …

Каждого рано или поздно мучает вопрос, а какое же самое большое число. На вопрос ребенка можно ответить миллион. А что дальше? Триллион. А еще дальше? На самом деле, ответ на вопрос какие же самые большие числа прост. К самому большому числу просто стоит добавить единицу, как оно уже не будет самым большим. Процедуру эту можно продолжать до бесконечности.

А если же задаться вопросом: какое самое большое число существует, и какое у него собственное название?

Сейчас мы все узнаем …

Существуют две системы наименования чисел — американская и английская.

Американская система постороена довольно просто. Все названия больших чисел строятся так: в начале идет латинское порядковое числительное, а в конце к ней добавляется суффикс -иллион. Исключение составляет название «миллион» которое является названием числа тысяча (лат. mille) и увеличительного суффикса -иллион (см. таблицу). Так получаются числа — триллион, квадриллион, квинтиллион, секстиллион, септиллион, октиллион, нониллион и дециллион. Американская система используется в США, Канаде, Франции и России. Узнать количество нулей в числе, записанном по американской системе, можно по простой формуле 3·x+3 (где x — латинское числительное).

Английская система наименования наиболее распространена в мире. Ей пользуются, например,

Большие числа — Википедия

Материал из Википедии — свободной энциклопедии

Неформально (обычно в развлекательной математике и научно-популярной литературе) большими числами называют числа, значительно превосходящие числа, используемые в повседневной жизни.

Изучение больших чисел и их номенклатуры иногда называются термином гугология (англ. googology)^[1]^[2]^[3]. Термин был образован как комбинация слов «гугол» (классическое большое число) и «логос» (учение). Термин введён любителем математики Джонатаном Бауэрсом^[2].

Несмотря на то что гугология — современный термин, история изучения человеком больших чисел уходит в глубокую древность.

III век до н. э. — Архимед в своём труде Псаммит представил нотацию, позволяющую записывать числа до 108×1016{\displaystyle 10^{8\times 10^{16}}}^[4]. В связи с этим его иногда называют первым «гугологистом»^[2].

I век н. э. — В буддистском священном тексте Аватамсака-сутра было упомянуто число ≈101032{\displaystyle \approx 10^{10^{32}}}

1928 год — Вильгельм Аккерман опубликовал свою функцию.

1940 год — Эдвард Казнер описал числа гугол (10100{\displaystyle 10^{100}}) и гуголплекс (1010100{\displaystyle 10^{10^{100}}})^[5].

1947 год — Р. Гудштейн^[en] дал наименование операциям тетрации (a↑↑b{\displaystyle a\uparrow \uparrow b}), пентации (a↑↑↑b{\displaystyle a\uparrow \uparrow \uparrow b}) и гексации (a↑4b{\displaystyle a\uparrow ^{4}b})^[6].

1970 год — С. Вайнер дал определение быстрорастущей иерархии^[7].

1976 год — Дональд Кнут изобрёл стрелочную нотацию^[8] (предел ω{\displaystyle \omega } в терминологии быстрорастущей иерархии).

1977 год — Мартин Гарднер в журнале Scientific American описал число Грэма^[9] (G=g(64)=f64(4){\displaystyle G=g(64)=f^{64}(4)}, где f(n)=3↑n3{\displaystyle f(n)=3\uparrow ^{n}3}. Функция g(n){\displaystyle g(n)} имеет скорость роста порядка ω+1{\displaystyle \omega +1}).

1983 год — была изобретена нотация Штейнгауза — Мозера^[10](предел ω{\displaystyle \omega }).

1995 год — Джон Конвей изобрёл цепную стрелочную нотацию^[11](предел ω2{\displaystyle \omega ^{2}}).

2002 год — Д. Бауэрс (J. Bowers) опубликовал свои нотацию массива^[12]^[13] (предел ωω{\displaystyle \omega ^{\omega }}) и расширенную нотацию массива (предел ωωω{\displaystyle \omega ^{\omega ^{\omega }}}).

2002 год — Х. Фридман^[en] дал определение функции TREE(n), имеющей скорость роста θ(Ωωω){\displaystyle \theta (\Omega ^{\omega }\omega )}.

2006 год — Х. Фридман дал определение быстрорастущим функциям SCG(n) и SSCG(n).

2007 год — Бауэрс определил ещё более мощную нотацию BEAF (данная нотация хорошо определена до ε0{\displaystyle \varepsilon _{0}}, числа, превосходящие этот уровень, вызывают противоречивость оценок).

Математические объекты, имеющие отношения к гугологии (в том числе большие числа), называются гугологизмами. В настоящее время наименования даны для нескольких тысяч чисел, превосходящих гугол. Ниже приведён список некоторых гугологизмов и их выражения в наиболее известных нотациях^[14]. Перед выражением в той нотации, в которой число было записано автором, стоит знак равенства, выражения для того же числа в других нотациях представляют собой аппроксимации.

имя числа	степень десяти	нотация Кнута	нотация Конвея	Нотация Бауэрса (нотация массива)	Нотация Сайбиана (гипер-E нотация)	быстрорастущая иерархия
Гугол	=10100{\displaystyle =10^{100}}	10↑100{\displaystyle 10\uparrow 100}	10→100{\displaystyle 10\rightarrow 100}	{10,100}{\displaystyle \{10,100\}}	E100{\displaystyle E100}	f2(324){\displaystyle f_{2}(324)}
Гуголплекс	=1010100{\displaystyle =10^{10^{100}}}	10↑10↑100{\displaystyle 10\uparrow 10\uparrow 100}	10→(10→100){\displaystyle 10\rightarrow (10\rightarrow 100)}	{10,{10,100}}{\displaystyle \{10,\{10,100\}\}}	E100#2{\displaystyle E100\#2}	f22(324){\displaystyle f_{2}^{2}(324)}
Гиггол (Giggol)	101010⋯1010⏟100 десяток{\displaystyle \underbrace {10^{10^{10^{\cdots ^{10^{10}}}}}} _{\text{100 десяток}}}	10↑2100{\displaystyle 10\uparrow ^{2}100}	10→100→2{\displaystyle 10\rightarrow 100\rightarrow 2}	={10,100,2}{\displaystyle =\{10,100,2\}}	E1#100{\displaystyle E1\#100}	f3(100){\displaystyle f_{3}(100)}
Гаггол (Gaggol)	101010⋯1010⏟101010⋯1010⏟⋮⏟101010⋯1010⏟10 десяток}100 {\displaystyle \left.{\begin{matrix}&&\underbrace {10^{10^{10^{\cdots ^{10^{10}}}}}} \\&&\underbrace {10^{10^{10^{\cdots ^{10^{10}}}}}} \\&&\underbrace {\quad \quad \;\;\vdots \quad \quad \;\;} \\&&\underbrace {10^{10^{10^{\cdots ^{10^{10}}}}}} \\&&{\text{10 десяток}}\end{matrix}}\right\}{\text{100 }}}	10↑3100{\displaystyle 10\uparrow ^{3}100}	10→100→3{\displaystyle 10\rightarrow 100\rightarrow 3}	={10,100,3}{\displaystyle =\{10,100,3\}}	E1#1#100{\displaystyle E1\#1\#100}	f4(100){\displaystyle f_{4}(100)}
Бугол (Boogol)		10↑10010{\displaystyle 10\uparrow ^{100}10}	10→10→100{\displaystyle 10\rightarrow 10\rightarrow 100}	={10,10,100}{\displaystyle =\{10,10,100\}}	E100##100{\displaystyle E100\#\#100}	f101(100){\displaystyle f_{101}(100)}
Число Грэма		=3↑↑⋯↑↑3⏟3↑↑⋯↑↑3⏟⋮⏟3↑↑⋯↑↑3⏟3↑43стрелок}64 {\displaystyle =\left.{\begin{matrix}&&\underbrace {3\uparrow \uparrow \cdots \uparrow \uparrow 3} \\&&\underbrace {3\uparrow \uparrow \cdots \uparrow \uparrow 3} \\&&\underbrace {\quad \quad \;\;\vdots \quad \quad \;\;} \\&&\underbrace {3\uparrow \uparrow \cdots \uparrow \uparrow 3} \\&&3\uparrow ^{4}3{\text{стрелок}}\end{matrix}}\right\}{\text{64 }}}	3→3→64→2{\displaystyle 3\rightarrow 3\rightarrow 64\rightarrow 2}	{3,65,1,2}{\displaystyle \{3,65,1,2\}}	E(3)3##4#64{\displaystyle E(3)3\#\#4\#64}	fω+1(64){\displaystyle f_{\omega +1}(64)}
Траддом (Traddom)^[15]			10→10→11→4{\displaystyle 10\rightarrow 10\rightarrow 11\rightarrow 4}	{10,10,3,2}{\displaystyle \{10,10,3,2\}}	E10##10##4{\displaystyle E10\#\#10\#\#4}	=fω+3(10){\displaystyle =f_{\omega +3}(10)}
Биггол (Biggol)			10→10→10→100{\displaystyle 10\rightarrow 10\rightarrow 10\rightarrow 100}	={10,10,100,2}{\displaystyle =\{10,10,100,2\}}	E100##100##100{\displaystyle E100\#\#100\#\#100}	fω.2(100){\displaystyle f_{\omega .2}(100)}
Трултом (Trultom)			10→10→10→10→11{\displaystyle 10\rightarrow 10\rightarrow 10\rightarrow 10\rightarrow 11}	{10,10,10,3}{\displaystyle \{10,10,10,3\}}	E10###4{\displaystyle E10\#\#\#4}	=fω.3(10){\displaystyle =f_{\omega .3}(10)}
Тругол (Troogol)			10→10→⋯→10⏟101→{\displaystyle \underbrace {10\rightarrow 10\rightarrow \cdots \rightarrow 10} _{101\quad \rightarrow }}	={10,10,10,100}{\displaystyle =\{10,10,10,100\}}	E100###100{\displaystyle E100\#\#\#100}	fω2(100){\displaystyle f_{\omega ^{2}}(100)}

Числа, приведённые ниже, находятся уже за пределами применения нотаций Кнута и Конвея.

имя числа	нотация Бауэрса (BEAF)	нотация Сайбиана	быстрорастущая иерархия
Квадругол (Quadroogol)	={10,10,10,10,100}{\displaystyle =\{10,10,10,10,100\}}	E100####100{\displaystyle E100\#\#\#\#100}	fω3(100){\displaystyle f_{\omega ^{3}}(100)}
Квадрексом (Quadrexom)	{10,10,10,10,10,10}{\displaystyle \{10,10,10,10,10,10\}}	E10#####10{\displaystyle E10\#\#\#\#\#10}	=fω4(10){\displaystyle =f_{\omega ^{4}}(10)}
Квинтугол (Quintoogol)	={10,10,10,10,10,100}{\displaystyle =\{10,10,10,10,10,100\}}	E100#####100{\displaystyle E100\#\#\#\#\#100}	fω4(100){\displaystyle f_{\omega ^{4}}(100)}
Губол (Goobol)	={10,100(1)2}={\displaystyle =\{10,100(1)2\}=} ={10,10,10,⋯,10,10}⏟100десяток{\displaystyle =\underbrace {\{10,10,10,\cdots ,10,10\}} _{100\quad {\text{десяток}}}}	E100#99100{\displaystyle E100\#^{99}100}	fω98(100){\displaystyle f_{\omega ^{98}}(100)}
Бубол (Boobol)	={10,10,100(1)2}{\displaystyle =\{10,10,100(1)2\}}	E100#^#100##100	fωω+99(100){\displaystyle f_{\omega ^{\omega }+99}(100)}
Трубол (Troobol)	={10,10,10,100(1)2}{\displaystyle =\{10,10,10,100(1)2\}}	E100#^#100###101	fωω+ω2(100){\displaystyle f_{\omega ^{\omega }+\omega ^{2}}(100)}
Квадрубол (Quadroobol)	={10,10,10,10,100(1)2}{\displaystyle =\{10,10,10,10,100(1)2\}}	E100#^#100####101	fωω+ω3(100){\displaystyle f_{\omega ^{\omega }+\omega ^{3}}(100)}
Гутрол (Gootrol)	={10,100(1)3}{\displaystyle =\{10,100(1)3\}}	E100#^#100#^#100	fωω.2(100){\displaystyle f_{\omega ^{\omega }.2}(100)}
Госсол (Gossol)	={10,10(1)100}{\displaystyle =\{10,10(1)100\}}	E100#^#*#100	fωω+1(100){\displaystyle f_{\omega ^{\omega +1}}(100)}
Моссол (Mossol)	={10,10(1)10,100}{\displaystyle =\{10,10(1)10,100\}}	E100#^#*##100	fωω+2(100){\displaystyle f_{\omega ^{\omega +2}}(100)}
Боссол (Bossol)	={10,10(1)10,10,100}{\displaystyle =\{10,10(1)10,10,100\}}	E100#^#*###100	fωω+3(100){\displaystyle f_{\omega ^{\omega +3}}(100)}
Троссол (Trossol)	={10,10(1)10,10,10,100}{\displaystyle =\{10,10(1)10,10,10,100\}}	E100#^#*####100	fωω+4(100){\displaystyle f_{\omega ^{\omega +4}}(100)}
Дубол (Dubol)	={10,100(1)(1)2}{\displaystyle =\{10,100(1)(1)2\}}	E100#^#*#^#100	fωω.2(100){\displaystyle f_{\omega ^{\omega .2}}(100)}
Дутрол (Dutrol)	={10,100(1)(1)3}{\displaystyle =\{10,100(1)(1)3\}}	E100#^##^#100#^##^#100	fωω.2.2(100){\displaystyle f_{\omega ^{\omega .2}.2}(100)}
Колоссол (Colossol)	={10,10(3)2}{\displaystyle =\{10,10(3)2\}}	E10#^###10	fωω3(10){\displaystyle f_{\omega ^{\omega ^{3}}}(10)}
Тероссол (Terossol)	={10,10(4)2}{\displaystyle =\{10,10(4)2\}}

Как называется самое большое число в мире

Содержание статьи:

ТОП-10 самых больших известных чисел

Как показывает практика, предельного понятия исчисления нет. Когда дети задают вопрос о том, какое самое большое число, ответить можно только в рамках абстрактного понятия.

Чтобы разобраться в этом вопросе и улучшить кругозор, можно изучить ТОП-10 самых больших известных чисел, которые известны человечеству на сегодняшний день.

10^80

Известно как 10 с 80 нулями. В Америке и на территории Англии называют — квинквавигинтиллион. Казалось бы, что может быть больше, ведь это число может охарактеризовать количество частиц во вселенной.

Однако 10 в 80-ой степени далеко не самое большое значение, которое на сегодняшний день известно ученым.

Гугол

Интересный факт, всеми известная поисковая система подарила этому числу большую популярность. Однако значение известно лишь истинным фанатам. Говоря о том, сколько это на самом деле можно выделить число со 100-та нулями.

Термин был придуман в 1938 году, автором стал Милтон Сиротта, которому было всего 9 лет. Существует теория, что когда возраст Земли достигнет гугла, во Вселенной произойдет взрыв черной дыры, что позволит изучить границы за ее пределами.

8,5 х 10^185

С одной стороны это значение обозначает самую маленькую характеристику длины, а с другой это одно из самых больших чисел. В науке обозначается как Длина Планка.

В отличие от других значений имеет распространение в квантовой физике и стала частью теории струн. Говоря о том, сколько же это число значит, можно выделить — 0,00000000000000000000000000000616199 метра.

2^43,112,609 – 1

Интересный факт — в этом числе практически 18 миллионов цифр. Обнаружили сравнительно недавно, т.е в 2008 году в ходе GIMPS.

Несмотря на свою величину, занимает лишь 47 место в порядке размера.

Гуголплекс

Впервые те, кто не сталкивался плотно с наукой, могли услышать это значение в фильме «Назад Будущее». Во время одного из мозговых штурмов Эммет Браун обронил слово Гуголплекс.

Как показали успешные поиски фанатов — такое значение существует. Гуголплекс — равен 10-ти в степени гугол. Для абстрактного понятия можно представить, что эта сумма больше чем частиц во Вселенной, которые были изучены за все существование науки.

Числа Скьюза

Достаточно много теорий по поводу величины этого значений. Однако если взять за основу самую популярную, то окажется, что Скьюз больше чем гуголплекс в несколько раз. Джон Литтлвуд в далеком 1914 году делал первые открытия, которые доказывали существование этого числа.

Однако доказать значение получилось только у Стенли Скьюза в 1933, после того, как он взял в основу теорию Римана.

Теория Пуанкаре

Число и одновременно теория о том, сколько бы времени понадобилось бы нашей Вселенной, что вернуться в исходное состояние.

Говоря простым языком, 10^10^10^10^10^1,1 лет нужно для того, чтобы история человечества вновь повторилась.

Значение Грэма

Одно из самых больших чисел, которое стало известно лишь в конце 80-х. Для его простой записи используют метод Кнута. Запомнить написание практически невозможно. Чтобы оценить масштабность значения, можно представить как число Пуанкаре умножают на несколько раз.

Особенность Грэма заключается в том, что для записи использую несколько уровней, самая простая выглядит так: G=f64(4), где f(n)=3↑^n3.

Если разбирать слои, то можно понять 3↑↑↑↑3 это уже больше чем число Пуанкаре. Одни из интересных фактов — первые числа пока неизвестно миру, а вот последние (всего 10) Грэм все же успел вычислить — 2464195387.

Бесконечность

С научной точки зрения число имеет огромную величину. Она настолько большая, что порой человеческой возможности абстракции не хватает фантазии чтобы ее представить.

Интересный факт, бесконечность ровно на половину делится на четные и нечетные числа. Ученые сами до конца не выяснили до конца какую величину обозначает мера «бесконечность». Ведь сегодня известно лишь 10^80 частиц.

Также значение бесконечности доказывает, что если вся вселенная устроена по принципу земли — т.е атомы складываются рано или поздно воедино, это значит копия планеты в теории может существовать. Более того, дублироваться может и сама вселенная.

Однако в такую теорию верят далеко не все ученые, например Дорон Зильбергер из Израиля настаивает на то, что вскоре найдется число больше бесконечности.

Когда это произойдет не уточняется, ведь предельное число бесконечности лишь абстрактное понимание. Тем не менее на сегодняшний день именно о бесконечности говорят в школах, и именно это значение является верховным в математической философии.

∞ + 1

Несмотря на абстрактность теории о бесконечности, есть идея, что это не конечное число. Как показывает практика, у каждого числа есть своя принадлежность, т.е к плюсу или минусу.

Если из суммы натуральных чисел вычесть сумму их квадрата — можно получить — ∞. Это значит, что границы бесконечности не могут заканчиваться только на одной теории о конечном числе. Чтобы углубиться в этот вопрос можно изучить метод Лопиталя.

Самое большое число в мире

Продолжаем нашу рубрику САМОГО САМОГО. Сегодня у нас числа …

А если же задаться вопросом: какое самое большое число существует, и какое у него собственное название? Сейчас мы все узнаем …

Существуют две системы наименования чисел — американская и английская.

Английская система наименования наиболее распространена в мире. Ей пользуются, например, в Великобритании и Испании, а также в большинстве бывших английских и испанских колоний. Названия чисел в этой системе строятся так: так: к латинскому числительному добавляют суффикс -иллион, следущее число (в 1000 раз большее) строится по принципу — то же самое латинское числительное, но суффикс — -иллиард. То есть после триллиона в английской системе идёт триллиард, а только затем квадриллион, за которым следует квадриллиард и т.д. Таким образом, квадриллион по английской и американской системам — это совсем разные числа! Узнать количество нулей в числе, записанном по английской системе и оканчивающегося суффиксом -иллион, можно по формуле 6·x+3 (где x — латинское числительное) и по формуле 6·x+6 для чисел, оканчивающихся на -иллиард.

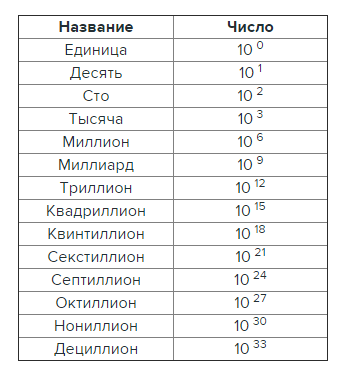
Из английской системы в русский язык перешло только число миллиард (10 9), которое всё же было бы правильнее называть так, как его называют американцы — биллионом, так как у нас принята именно американская система. Но кто у нас в стране что-то делает по правилам! 😉 Кстати, иногда в русском языке употребляют и слово триллиард (можете сами в этом убедиться, запустив поиск в Гугле или Яндексе) и означает оно, судя по всему, 1000 триллионов, т.е. квадриллион.

Кроме чисел, записанных при помощи латинских префиксов по американской или англйской системе, известны и так называемые внесистемные числа, т.е. числа, которые имеют свои собственные названия безо всяких латинских префиксов. Таких чисел существует несколько, но подробнее о них я расскажу чуть позже.

Вернемся к записи при помощи латинских числительных. Казалось бы, что ими можно записывать числа до бессконечности, но это не совсем так. Сейчас объясню почему. Посмотрим для начала как называются числа от 1 до 10 33:

И вот, теперь возникает вопрос, а что дальше. Что там за дециллионом? В принципе, можно, конечно же, при помощи объединения приставок породить такие монстры, как: андецилион, дуодециллион, тредециллион, кваттордециллион, квиндециллион, сексдециллион, септемдециллион, октодециллион и новемдециллион, но это уже будут составные названия, а нам были интересны именно собственные названия чисел. Поэтому собственных имён по этой системе, помимо указанных выше, ещё можно получить лишь всего три — вигинтиллион (от лат. viginti — двадцать), центиллион (от лат. centum — сто) и миллеиллион (от лат. mille — тысяча). Больше тысячи собственных названий для чисел у римлян не имелось (все числа больше тысячи у них были составными). Например, миллион (1 000 000) римляне называли decies centena milia, то есть «десять сотен тысяч». А теперь, собственно, таблица:

Таким образом, по подобной системе числа больше, чем 10 3003, у которого было бы собственное, несоставное название получить невозможно! Но тем не менее числа больше миллеиллиона известны — это те самые внесистемные числа. Расскажем, наконец-то, о них.

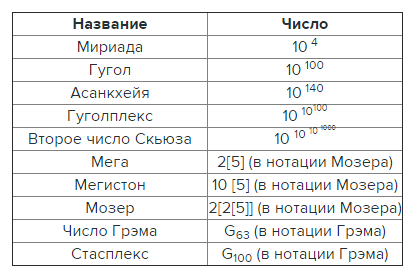
Самое маленькое такое число — это мириада (оно есть даже в словаре Даля), которое означает сотню сотен, то есть — 10 000. Слово это, правда, устарело и практически не используется, но любопытно, что широко используется слово «мириады», которое означает вовсе не определённое число, а бесчисленное, несчётное множество чего-либо. Считается, что слово мириада (англ. myriad) пришло в европейские языки из древнего Египта.

Насчёт происхождения этого числа существуют разные мнения. Одни считают, что оно возникло в Египте, другие же полагают, что оно родилось лишь в Античной Греции. Как бы то ни было на самом деле, но известность мириада получила именно благодаря грекам. Мириада являлось названием для 10 000, а для чисел больше десяти тысяч названий не было. Однако в заметке «Псаммит» (т.е. исчисление песка) Архимед показал, как можно систематически строить и называть сколь угодно большие числа. В частности, размещая в маковом зерне 10 000 (мириада) песчинок, он находит, что во Вселенной (шар диаметром в мириаду диаметров Земли) поместилось бы (в наших обозначениях) не более чем 1063песчинок. Любопытно, что современные подсчеты количества атомов в видимой Вселенной приводят к числу 1067 (всего в мириаду раз больше). Названия чисел Архимед предложил такие:
1 мириада = 104.
1 ди-мириада = мириада мириад = 108.
1 три-мириада = ди-мириада ди-мириад = 1016.
1 тетра-мириада = три-мириада три-мириад = 1032.
и т.д.

Гугол (от англ. googol) — это число десять в сотой степени, то есть единица со ста нулями. О «гуголе» впервые написал в 1938 году в статье «New Names in Mathematics» в январском номере журнала Scripta Mathematica американский математик Эдвард Каснер (Edward Kasner). По его словам, назвать «гуголом» большое число предложил его девятилетний племянник Милтон Сиротта (Milton Sirotta). Общеизвестным же это число стало благодаря, названной в честь него, поисковой машине Google. Обратите внимание, что «Google» — это торговая марка, а googol — число.

Эдвард Каснер (Edward Kasner).

В интернете вы часто можете встретить упоминание, что Гугол самое большое число в мире — но это не так …

В известном буддийском трактате Джайна-сутры, относящегося к 100 г. до н.э., встречается число асанкхейя (от кит. асэнци — неисчислимый), равное 10 140. Считается, что этому числу равно количество космических циклов, необходимых для обретения нирваны.

Гуголплекс (англ. googolplex) — число также придуманное Каснером со своим племянником и означающее единицу с гуголом нулей, то есть 10

Названия больших чисел и количество нулей в них

3	10³	тясяча	thousand
6	10⁶	миллион	million
9	10⁹	миллиард (биллион)	billion
12	10¹²	триллион	trillion
15	10¹⁵	квадриллион	quadrillion
18	10¹⁸	квинтиллион	quintillion
21	10²¹	секстиллион	sextillion
24	10²⁴	септиллион	septillion
27	10²⁷	октиллион	octillion
30	10³⁰	нониллион	nonillion
33	10³³	дециллион	decillion
36	10³⁶	ундециллион	undecillion
39	10³⁹	дуодециллион	duodecillion
42	10⁴²	тредециллион	tredecillion
45	10⁴⁵	кватуордециллион	quattuordecillion
48	10⁴⁸	квиндециллион	quindecillion
51	10⁵¹	сексдециллион	sexdecillion
54	10⁵⁴	септендециллион	septendecillion
57	10⁵⁷	октодециллион	octodecillion
60	10⁶⁰	новемдециллион	novemdecillion
63	10⁶³	вигинтиллион	vigintillion
66	10⁶⁶	унвигинтиллион	unvigintillion
69	10⁶⁹	дуовигинтиллион	duovigintillion
72	10⁷²	тревигинтиллион	trevigintillion
75	10⁷⁵	кватуорвигинтиллион	quattuorvigintillion
78	10⁷⁸	квинвигинтиллион	quinvigintillion
81	10⁸¹	сексвигинтиллион	sexvigintillion
84	10⁸⁴	септенвигинтиллион	septenvigintillion
87	10⁸⁷	октовигинтиллион	octovigintillion
90	10⁹⁰	новемвигинтиллион	novemvigintillion
93	10⁹³	тригинтиллион	trigintillion
96	10⁹⁶	унтригинтиллион	untrigintillion
99	10⁹⁹	дуотригинтиллион	duotrigintillion
102	10¹⁰²	третригинтиллион	trestrigintillion
105	10¹⁰⁵	кватортригинтиллион	quattuortrigintillion
108	10¹⁰⁸	квинтригинтиллион	quintrigintillion
111	10¹¹¹	секстригинтиллион	sextrigintillion
114	10¹¹⁴	септентригинтиллион	septentrigintillion
117	10¹¹⁷	октотригинтиллион	octotrigintillion
120	10¹²⁰	новемтригинтиллион	novemtrigintillion
123	10¹²³	квадрагинтиллион	quadragintillion
126	10¹²⁶	унквадрагинтиллион	unquadragintillion
129	10¹²⁹	дуоквадрагинтиллион	duoquadragintillion
132	10¹³²	треквадрагинтиллион	trequadragintillion
135	10¹³⁵	кваторквадрагинтиллион	quattuorquadragintillion
138	10¹³⁸	квинквадрагинтиллион	quinquadragintillion
141	10¹⁴¹	сексквадрагинтиллион	sexquadragintillion
144	10¹⁴⁴	септенквадрагинтиллион	septenquadragintillion
147	10¹⁴⁷	октоквадрагинтиллион	octoquadragintillion
150	10¹⁵⁰	новемквадрагинтиллион	novemquadragintillion
153	10¹⁵³	квинквагинтиллион	quinquagintillion
156	10¹⁵⁶	унквинкагинтиллион	unquinquagintillion
159	10¹⁵⁹	дуоквинкагинтиллион	duoquinquagintillion
162	10¹⁶²	треквинкагинтиллион	trequinquagintillion
165	10¹⁶⁵	кваторквинкагинтиллион	quattuorquinquagintillion
168	10¹⁶⁸	квинквинкагинтиллион	quinquinquagintillion
171	10¹⁷¹	сексквинкагинтиллион	sexquinquagintillion
174	10¹⁷⁴	септенквинкагинтиллион	septenquinquagintillion
177	10¹⁷⁷	октоквинкагинтиллион	octoquinquagintillion
180	10¹⁸⁰	новемквинкагинтиллион	novemquinquagintillion
183	10¹⁸³	сексагинтиллион	sexagintillion
186	10¹⁸⁶	унсексагинтиллион	unsexagintillion
189	10¹⁸⁹	дуосексагинтиллион	duosexagintillion
192	10¹⁹²	тресексагинтиллион	tresexagintillion
195	10¹⁹⁵	кваторсексагинтиллион	quattuorsexagintillion
198	10¹⁹⁸	квинсексагинтиллион	quinsexagintillion
201	10²⁰¹	секссексагинтиллион	sexsexagintillion
204	10²⁰⁴	септенсексагинтиллион	septensexagintillion
207	10²⁰⁷	октосексагинтиллион	octosexagintillion
210	10²¹⁰	новемсексагинтиллион	novemsexagintillion
213	10²¹³	септагинтиллион	septuagintillion
216	10²¹⁶	унсептагинтиллион	unseptuagintillion
219	10²¹⁹	дуосептагинтиллион	duoseptuagintillion
222	10²²²	тресептагинтиллион	treseptuagintillion
225	10²²⁵	кваторсептагинтиллион	quattuorseptuagintillion
228	10²²⁸	квинсептагинтиллион	quinseptuagintillion
231	10²³¹	секссептагинтиллион	sexseptuagintillion
234	10²³⁴	септенсептагинтиллион	septenseptuagintillion
237	10²³⁷	октосептагинтиллион	octoseptuagintillion
240	10²⁴⁰	новемсептагинтиллион	novemseptuagintillion
243	10²⁴³	октогинтиллион	octogintillion
246	10²⁴⁶	уноктогинтиллион	unoctogintillion
249	10²⁴⁹	дуооктогинтиллион	duooctogintillion
252	10²⁵²	треоктогинтиллион	treoctogintillion
255	10²⁵⁵	кватороктогинтиллион	quattuoroctogintillion
258	10²⁵⁸	квиноктогинтиллион	quinoctogintillion
261	10²⁶¹	сексоктогинтиллион	sexoctogintillion
264	10²⁶⁴	септоктогинтиллион	septoctogintillion
267	10²⁶⁷	октооктогинтиллион	octooctogintillion
270	10²⁷⁰	новемоктогинтиллион	novemoctogintillion
273	10²⁷³	нонагинтиллион	nonagintillion
276	10²⁷⁶	уннонагинтиллион	unnonagintillion
279	10²⁷⁹	дуононагинтиллион	duononagintillion
282	10²⁸²	тренонагинтиллион	trenonagintillion
285	10²⁸⁵	кваторнонагинтиллион	quattuornonagintillion
288	10²⁸⁸	квиннонагинтиллион	quinnonagintillion
291	10²⁹¹	секснонагинтиллион	sexnonagintillion
294	10²⁹⁴	септеннонагинтиллион	septennonagintillion
297	10²⁹⁷	октононагинтиллион	octononagintillion
300	10³⁰⁰	новемнонагинтиллион	novemnonagintillion
303	10³⁰³	центиллион	centillion

Самое большое число — 24СМИ

Из школьного курса известно, что наибольшего числа не существует. Ведь если к самому большому числу прибавить хотя бы единицу, то получим еще большее число. Школьник с легкостью скажет, что, например, самое большое двузначное число — 99, а трехзначное — 999 и т.д.

Существует два алгоритма наименования чисел – английский и американский.

В американском названия больших чисел строятся следующим образом: сначала идет латинское порядковое числительное, а затем добавляется суффикс «иллион». Исключение – миллион. Далее получаются числа: триллион, квадриллион, квинтиллион. После идут секстиллион, септиллион, октиллион, нониллион и дециллион. Такой способ используют в США, Канаде, России и Франции.

Американский алгоритм наименования чисел

Английский алгоритм используют в Испании и Великобритании, а так же в ряде бывших колоний. Здесь названия строятся так: к латинскому числительному прибавляют суффикс «иллион», к следующему числу (которое больше в 1000 раз) уже добавляют суффикс «иллиард». После триллиона идет триллиард, после квадриллион, квадриллиард и т.д. Получается, что по английскому и американскому алгоритму одни и те же большие числа называются по-разному.

Читайте по теме: Самое маленькое число

В русский язык из английской системы пришел только миллиард (109), который американцы называют биллионом. Иногда в России употребляют слово триллиард, т.е. 1000 триллионов или квадриллион.

Самое большое число

Самое большое простое число в мире – 274207281 – 1, которое содержит 22 338 618 десятичных цифр (простое число Мерсенна). Значение нашли в 2015 году в ходе проекта по распределенному поиску простых чисел Мерсенна GIMPS. Поясним, что простыми называются натуральные (целые положительные) числа, имеющие только два делителя — единицу и само себя. Например, 2, 3, 5, 7 — простые числа. Список продолжают 11, 13, 17, 19… Кроме двойки все числа нечетные, иначе бы делились не только на единицу и себя, но и на два. Значит, найденное простое число еще и самое большое из нечетных.

Маренн Марсен и самое большое простое число

По утверждению Евклида, простых чисел бесконечное множество, значит, наибольшего простого числа нет. Ученые до сих пор ищут числа-рекордсмены. И тому есть разумное объяснение. Всемирная организация Electronic Frontier Foundation учредила награды за подобные открытия: чем больше найденное число, тем выше награда.

Есть специальный способ проверки простоты чисел, который называется тест Люка-Лемера. Правда, предназначен он исключительно для чисел Мерсенна. Что же это за числа? Это вид натуральных чисел, расположенных в определенной последовательности. Имя им дал французский математик Мерсенн Марен. Вид числа Мерсенна такой:

Mn = 2n – 1,

где n — натуральное число.

При n = 1, 2, 3, 4, … числа Мерсенна образуют последовательность, начинающуюся с 1, 3, 7, 15. Затем идут 31, 63, 127. Продолжают ряд 255, 511, 1023, 2047 и т.д.

Такие числа используют в криптографии, например, для усовершенствования банковских кодов.

Внесистемные числа

Кроме чисел, которые записаны при помощи английской или американской систем, известны внесистемные числа. У них есть собственные названия, в которых нет латинских префиксов. Для понимания сначала рассмотрим запись латинскими числительными.

Единица – это 100, десять — 101 и так далее: миллиард — 109, триллион — 1012, квадриллион — 1015, квинтиллион — 1018, секстиллион — 1021, септиллион — 1024, октиллион — 1027, нониллион — 1030, дециллион — 1033.

С помощью приставок можно и дальше выводить числа: андециллион, дуодециллион, тридециллион и так далее. Но нужны собственные названия чисел, а тут только составные названия. Поэтому по этой системе собственных имен еще только три — вигинтиллион — 1063, центиллион — 10303, миллеиллион — 103003.

В миллеиллионе 3003 нуля

Число с собственным, а не составным названием больше 103003 получить невозможно. Однако числа больше миллеиллиона известны – это внесистемные числа.

Самое маленькое внесистемное число носит название мириада. Означает сотню сотен, т.е. 10000.

Далее идет гугол. Это десять в сотой степени — 1010100. Единица со ста нулями. О гуголе впервые написали в 1938 году. Американский математик Эдвард Каснер сказал, что назвать большое число таким образом предложил племянник. А популярным это название стало после того, как в честь него назвали поисковик «Google».

Число гугол

Далее встречается число асанкхейя. Это 1010140. Следом идет число гуголплекс. Его придумал тот же Каснер с племянником. Означает 10 в степени 10 в степени 100. Или единица с гуголом нулей.

Еще больше гуголплекса число Скьюза. Его предложил Скьюз в 1933 году во время доказательства гипотезы Риманна о простых числах.

Обозначается — Sk1.

Есть второе число Скьюза. Обозначается как Sk2. Вводится, если гипотеза Риманна не справедлива. Второе число Скьюза равно

Но и это число не предел. Самое большое число, которое применяется в математическом доказательстве, это число Грэма. Его использовали впервые в 1977 году в доказательстве оценки в теории Рамсея.

Число выражено в 64-уровневой схеме, вывел которую Кнут в 1978 году. Ученый придумал понятие сверхстепень и предложил записывать ее стрелками вверх. В итоге число Грэма G63, или просто G, — самое большое число в мире. G даже попало в Книгу рекордов Гиннеса. Последние 50 цифр числа Грэма выглядят так: …03222348723967018485186439059104575627262464195387.

Доска объявлений Краснодар

Самая большая сумма – Самая большая банкнота в мире по номиналу и покупательной способности

Системы наименования чисел — Википедия

Таблица от значения к названию[править | править код]

Таблица от названия к значению[править | править код]

Самое большое число в мире

Большие числа — Википедия